lecture2-cs231n
Loss Function
在上一节定义了从图像像素值到所属类别的评分(score function),该函数的参数是权重矩阵W。在函数中,数据(Xi,Yi)是给定的,不能修改。但是我们可以调整权重矩阵这个参数,使得评分函数的结果与训练数据集中图像的真实类别一致,即评分函数在正确的分类的位置应当得到最高的评分(score)。
回到之前那张猫的图像分类例子,它有针对“猫”,“狗”,“船”三个类别的分数。我们看到例子中权重值非常差,因为猫分类的得分非常低(-96.8),而狗(437.9)和船(61.95)比较高。我们将使用损失函数(Loss Function)(有时也叫代价函数Cost Function或目标函数Objective)来衡量我们对结果的不满意程度。直观地讲,当评分函数输出结果与真实结果之间差异越大,损失函数输出越大,反之越小
多类支持向量机损失 Multiclass Support Vector Machine Loss
损失函数的具体形式多种多样。首先,介绍常用的多类支持向量机(SVM)损失函数。SVM的损失函数想要SVM在正确分类上的得分始终比不正确分类上的得分高出一个边界值delta。我们可以把损失函数想象成一个人,这位SVM先生(或者女士)对于结果有自己的品位,如果某个结果能使得损失值更低,那么SVM就更加喜欢它。

在结束这一小节前,还必须提一下的属于是关于0的阀值:
函数,它常被称为折叶损失(hinge loss)。有时候会听到人们使用平方折叶损失SVM(即L2-SVM),它使用的是
,将更强烈(平方地而不是线性地)地惩罚过界的边界值。不使用平方是更标准的版本,但是在某些数据集中,平方折叶损失会工作得更好。可以通过交叉验证来决定到底使用哪个。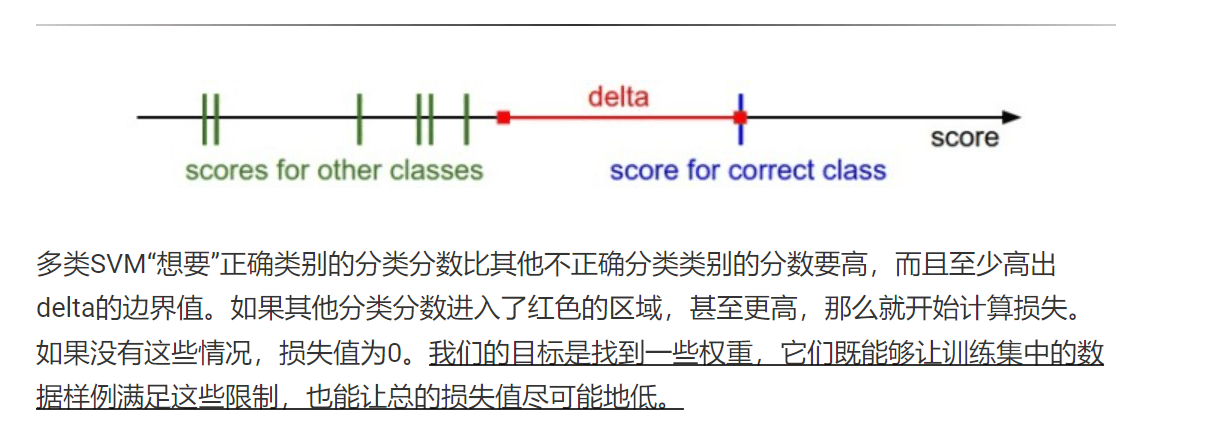
正则化(Regularization)

本课中展示的多类SVM只是多种SVM公式中的一种。
Softmax Classifier (Multinomial Logistic Regression)
interpret raw classifier scores as probabilities

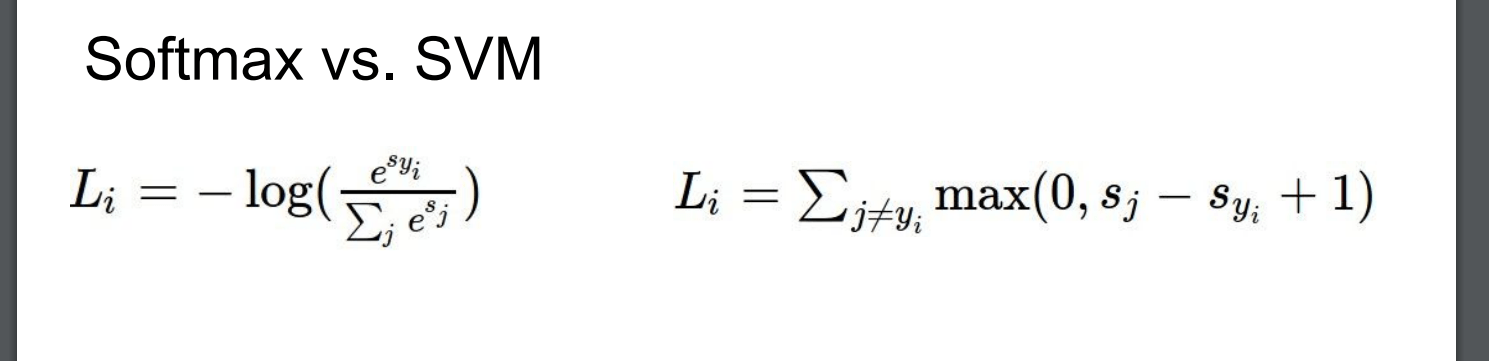
针对一个数据点,SVM和Softmax分类器的不同处理方式的例子。两个分类器都计算了同样的分值向量f(本节中是通过矩阵乘来实现)。不同之处在于对f中分值的解释:SVM分类器将它们看做是分类评分,它的损失函数鼓励正确的分类(本例中是蓝色的类别2)的分值比其他分类的分值高出至少一个边界值。Softmax分类器将这些数值看做是每个分类没有归一化的对数概率,鼓励正确分类的归一化的对数概率变高,其余的变低。SVM的最终的损失值是1.58,Softmax的最终的损失值是0.452,但要注意这两个数值没有可比性。只在给定同样数据,在同样的分类器的损失值计算中,它们才有意义。
还有,随着正则化参数λ不断增强,权重数值会越来越小,最后输出的概率会接近于均匀分布。这就是说,softmax分类器算出来的概率最好是看成一种对于分类正确性的自信。
在实际使用中,SVM和Softmax经常是相似的:通常说来,两种分类器的表现差别很小,不同的人对于哪个分类器更好有不同的看法。相对于Softmax分类器,SVM更加“局部目标化(local objective)”,这既可以看做是一个特性,也可以看做是一个劣势。考虑一个评分是[10, -2, 3]的数据,其中第一个分类是正确的。那么一个SVM(delta=1)会看到正确分类相较于不正确分类,已经得到了比边界值还要高的分数,它就会认为损失值是0。SVM对于数字个体的细节是不关心的:如果分数是[10, -100, -100]或者[10, 9, 9],对于SVM来说没什么不同,只要满足超过边界值等于1,那么损失值就等于0。
对于softmax分类器,情况则不同。对于[10, 9, 9]来说,计算出的损失值就远远高于[10, -100, -100]的。换句话来说,softmax分类器对于分数是永远不会满意的:正确分类总能得到更高的可能性,错误分类总能得到更低的可能性,损失值总是能够更小。但是,SVM只要边界值被满足了就满意了,不会超过限制去细微地操作具体分数。这可以被看做是SVM的一种特性。举例说来,一个汽车的分类器应该把他的大量精力放在如何分辨小轿车和大卡车上,而不应该纠结于如何与青蛙进行区分,因为区分青蛙得到的评分已经足够低了。
最优化 Optimization
损失函数可以量化某个具体权重集W的质量。而最优化的目标就是找到能够最小化损失函数值的W 。我们现在就朝着这个目标前进,实现一个能够最优化损失函数的方法。对于有一些经验的同学,这节课看起来有点奇怪,因为使用的例子(SVM 损失函数)是一个凸函数问题。但是要记得,最终的目标是不仅仅对凸函数做最优化,而是能够最优化一个神经网络,而对于神经网络是不能简单的使用凸函数的最优化技巧的。
核心思路:迭代优化。当然,我们肯定能做得更好些。核心思路是:虽然找到最优的权重W非常困难,甚至是不可能的(尤其当W中存的是整个神经网络的权重的时候),但如果问题转化为:对一个权重矩阵集W取优,使其损失值稍微减少。那么问题的难度就大大降低了。换句话说,我们的方法从一个随机的W开始,然后对其迭代取优,每次都让它的损失值变得更小一点。
我们的策略是从随机权重开始,然后迭代取优,从而获得更低的损失值。
蒙眼徒步者的比喻:一个助于理解的比喻是把你自己想象成一个蒙着眼睛的徒步者,正走在山地地形上,目标是要慢慢走到山底。在CIFAR-10的例子中,这山是30730维的(因为W是3073x10)。我们在山上踩的每一点都对应一个的损失值,该损失值可以看做该点的海拔高度。
我们是尝试在权重空间中找到一个方向,沿着该方向能降低损失函数的损失值。其实不需要随机寻找方向,因为可以直接计算出最好的方向,这就是从数学上计算出最陡峭的方向。这个方向就是损失函数的梯度(gradient)。在蒙眼徒步者的比喻中,这个方法就好比是感受我们脚下山体的倾斜程度,然后向着最陡峭的下降方向下山。
在一维函数中,斜率是函数在某一点的瞬时变化率。梯度是函数的斜率的一般化表达,它不是一个值,而是一个向量。在输入空间中,梯度是各个维度的斜率组成的向量(或者称为导数derivatives)。
梯度指明了函数在哪个方向是变化率最大的,但是没有指明在这个方向上应该走多远。在后续的课程中可以看到,选择步长(也叫作学习率)将会是神经网络训练中最重要(也是最头痛)的超参数设定之一。还是用蒙眼徒步者下山的比喻,这就好比我们可以感觉到脚朝向的不同方向上,地形的倾斜程度不同。但是该跨出多长的步长呢?不确定。如果谨慎地小步走,情况可能比较稳定但是进展较慢(这就是步长较小的情况)。相反,如果想尽快下山,那就大步走吧,但结果也不一定尽如人意。在上面的代码中就能看见反例,在某些点如果步长过大,反而可能越过最低点导致更高的损失值。
小批量数据梯度下降(Mini-batch gradient descent):在大规模的应用中(比如ILSVRC挑战赛),训练数据可以达到百万级量级。如果像这样计算整个训练集,来获得仅仅一个参数的更新就太浪费了。一个常用的方法是计算训练集中的 小批量(batches)数据。例如,在目前最高水平的卷积神经网络中,一个典型的小批量包含256个例子,而整个训练集是多少呢?一百二十万个。
梯度下降(Stochastic Gradient Descent 简称SGD),有时候也被称为在线梯度下降。这种策略在实际情况中相对少见,因为向量化操作的代码一次计算100个数据比100次计算1个数据要高效很多。即使SGD在技术上是指每次使用1个数据来计算梯度,你还是会听到人们使用SGD来指代小批量数据梯度下降(或者用MGD来指代小批量数据梯度下降,而BGD来指代则相对少见)。小批量数据的大小是一个超参数,但是一般并不需要通过交叉验证来调参。它一般由存储器的限制来决定的,或者干脆设置为同样大小,比如32,64,128等。之所以使用2的指数,是因为在实际中许多向量化操作实现的时候,如果输入数据量是2的倍数,那么运算更快。